L'ascenseur de M Einstein

On fête le centenaire de la publication de la relativité générale par Albert Einstein.

La relativité restreinte, exposée en 1905, est facile mathématiquement parlant, mais elle est complexe sur le plan conceptuel : c'est l'espace qui crée le temps, les vitesses relatives ne s'additionnent plus comme le disait M Galileo Galilei, la vitesse limite est celle de la lumière, et E = m c².

On n'a pas eu trop de difficultés à adapter les équations de Maxwell, qui sont stables par les transformations de Lorentz, et on peut même dire que la relativité restreinte en est une des conséquences, et faite pour. Mais pour la gravitation de Sir Isaac Newton, ça ne marchait pas du tout. That was the problem.

Tout ce qui était bien établi, c'est que la "distance" entre 2 événements est la même dans tous les référentiels si on la mesure avec la formule Ds² = c² Dt² - D x²- D y² - D z², c'est ce qu'on appelle la métrique de l'espace-temps.

Mais qu'en faire? Alors Einstein a inventé l'ascenseur qui tombe sans fin. Soit un ascenseur qui tombe et Einstein dedans, qui tient une pomme en réfléchissant. S'il lâche la pomme, elle reste devant lui sans bouger. Donc, quand on tombe avec/dans un ascenseur, on ne ressent aucune gravité.

Si un rayon de lumière, émis de l'extérieur, traverse la cabine de l'ascenseur par un trou, Einstein le verra décrire une sorte de parabole tournée vers le haut. Conclusion : la gravité n'est pas une force, puisque on ne peut la ressentir quand on tombe. Mais la gravité "déforme" l'espace-temps.

Donc le problème revient à se dire que si on veut étudier la gravitation dans un labo, on doit imaginer qu'elle est nulle dans un référentiel qui tombe, et qu'il suffit de transposer les équations dans le référentiel du labo, qui est accéléré vers le haut par rapport à l'autre. Coup de génie!

Après, ça se corse, car si on connait déjà la "métrique", on manque d'outils. Coup de chance les matheux, comme Riemann, Poincaré, et surtout Levi-Civita ont appris à traiter les espaces courbes et les tenseurs.
On pose donc ds² = gmn dx^mdxⁿ et gmn  est notre tenseur métrique : on appelle ça la "g-munutisation", et sa courbure doit être reliée à la structure de l'espace, le tenseur énergie-impulsion T^mn :

 avec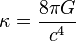 

La constante 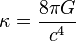 est facile à calculer : il suffit de considérer un univers plat, et on retrouve la bonne loi de Newton. C'est fait pour.

Avec Newton, les planètes tournaient autour du soleil, parce qu'il les "tirait". Avec Einstein, les planètes vont tout droit dans un univers courbe, comme une bille roule dans un bol.

La constante cosmologique L a toute une histoire : Einstein ne l'a mise que pour faire joli, ou plus exactement parce que sans elle, l'univers semblait avoir un commencement, ce qui le heurtait (en 1915). Et puis, on s'est aperçu que l'univers avait eu un commencement (en 1930), ou bien qu'il y avait création continue de matière. Einstein s'est excusé de "la plus grande erreur de sa vie". Et maintenant, on trouve qu'elle est bien, car elle expliquerait l’accélération de l'expansion de l'univers, la matière et l'énergie "noires". La suite au prochain épisode, que mes petits enfants découvriront peut-être.

En tout cas, ces calculs bizarroïdes ont été vite confirmés par l'expérience : ils expliquent l'avance du périhélie de Mercure, la déviation de la lumière autour des corps massifs, les lentilles gravitationnelles, et servent au calcul des GPS. Avec Newton, on calculait au millième, avec Einstein au milliardième....